도수 정렬은 요소의 대소 관계를 판단하지 않고 빠르게 정렬할 수 있는 알고리즘 입니다.
[도수 정렬]
1. 도수 정렬 알고리즘은 도수분포표 작성, 누적도수분포표 작성, 목적 배열 만들기, 배열 복사의 4단계로 이루어집니다.
<10점 만점의 테스트에서 학생 9명의 점수를 예로 들어 도수 정렬 알고리즘 만들기>
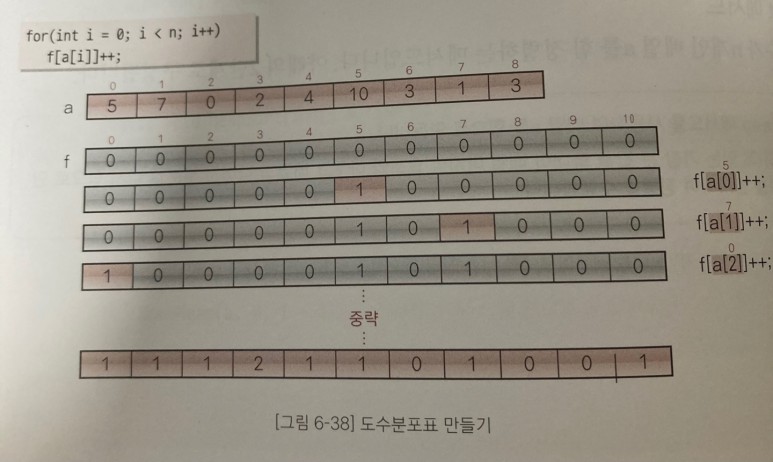
1) 1단계 도수분포표 만들기
(1) 배열 a를 바탕으로 '각 점수에 해당하는 학생이 몇 명인지를 나타내는 도수분포표 작성
(2) 도수분포표를 나타내기 위해 배열 f를 사용
(3) 먼저 배열 f의 모든 요소의 값을 0으로 초기화
(4) 그런 다음, 배열 a를 처음부터 스캔하면서 도수분포표를 만들면 됩니다.
2) 2단계 누적도수분포표 만들기
(1) '0점부터 점수 n까지 몇 명의 학생이 있는지' 누적된 값을 나타내는 도수분포표 만들기

예를들어, f[4]의 값(6)은 0~4점을 받은 학생이 6명임을 의미하고, f[10]의 값(9)은 0~10점을 받은 학생이 9명임을 의미합니다.
3) 목적 배열 만들기 ( 이 부분은 이해가 안가네요.)
(1) 배열의 각 요솟값과 누적도수분포표 f를 대조하여 정렬을 마친 배열을 만드는 작업하기
(2) 배열 a와 같은 요소의 개수를 갖는 작업용 배열 b가 필요합니다.
(3) 그러면, 배열 a의 요소를 마지막 위치부터 처음 위치까지 스캔하면서 배열 f와 대조하는 작업을 수행합니다.

☞ 마지막 요소(a[8])의 값은 3입니다. 누적도수를 나타내는 배열(f[3])의 값이 5이므로 0~3점 사이에 5명이 있음을 알 수 있습니다. 그러므로 목적 배열인 b[4]에 3을 저장합니다.

☞ 이 작업을 할 때 f[3]의 값을 5에서 1만큼 감소시켜 4로 만듭니다. 그 다음 바로 앞의 요소인 a[7[의 값은 1입니다. 누적도수를 나타내는 f[1]의 값(2)은 0~1점 사이에 2명이 있음을 의미합니다. 따라서 작업용 목적 배열 b[1]에 1을 저장합니다.
※ 배열의 2번째 요소는 인덱스가 1입니다. 따라서 이 작업을 할 때도 f[1]의 값을 2에서 1만큼 감소시켜 1로 만듭니다.

☞ 배열 a에서의 스캔을 계속 진행합니다. 다음에 살펴볼 값은 a[6]입니다. 이 때 a[8]에서 3점 학생을 배열 b에 저장하는 과정을 이미 한 번 진행했기 때문에 두 번째로 진행해야 합니다. 이때 a[8]의 값(3)을 목적 배열에 넣을 때 f[3]의 값을 1만큼 감소시켜 4로 만들었음을 기억하세요. 이렇게 미리 값을 감소시켰기 때문에 중복되는 값인 3을 목적 배열의 4번째 요소(b[3])에 저장할 수 있습니다.
4) 배열 복사하기
(1) 정렬은 끝났지만 정렬결과를 저장한 곳은 작업 배열(b)입니다.
배열 a는 정렬하기 전 상태이므로 배열 b 값을 배열 a로 복사해야 합니다.


☞ fSort 메서드는 정렬을 위한 작업용 배열 f와 b를 만듭니다.
도수 정렬 알고리즘은 데이터의 비교, 교환 작업이 필요 없어 매우 빠릅니다. 단일 for문만을 사용하며 재귀 호출, 이중 for문이 없어 아주 효율적인 알고리즘입니다. 하지만 도수분포표가 필요하기 때문에 데이터의 최솟값과 최댓값을 미리 알고 있는 경우에만 사용할 수 있습니다.
각 단계(for문)에서 배열 요소를 건너뛰지 않고 순서대로 스캔하기 때문에 같은 값에 대해서 순서가 바뀌는 일이 없어 이 정렬 알고리즘은 안정적이라고 할 수 있습니다. 그러나 3단계(목적 배열 만들기)에서 배열 a를 스캔할 때 마지막 위치부터가 아닌 처음부터 스캔을 하면 안정적이지 않습니다.