갈수록 난이도가 올라가네요..
따라쓰고 따라 치고 있지만.. 잘하고 있는건지.. 하는것에 의의를 둡니다..
힙 정렬은 선택 정렬을 응용한 알고리즘인 힙 정렬입니다.
[힙이란?]
1. 힙 정렬(heap sort)은 힙(heap)을 사용하여 정렬하는 알고리즘입니다. 힙은 '부모의 값이 자식의 값보다 항상 크다'는 조건을 만족하는 완전이진트리입니다. 이때 부모의 값이 자식보다 항상 작아도 힙이라고 합니다.
2. 힙의 요소를 배열에 저장하면 부모와 자식의 인덱스 사이에 다음과 같은 관계가 성립합니다.
1) 부모는 a[(i-1) / 2]
2) 왼쪽 자식은 a[i*2 + 1]
3) 오른쪽 자식은 a[i * 2 + 2]

[힙 정렬]
1. 힙 정렬은 '가장 큰 값이 루트에 위치'하는 특징을 이용하는 정렬 알고리즘입니다.
2. 힙에서 가장 큰 값인 루트를 꺼내는 작업을 반복하고 그 값을 늘어놓으면 배열은 정렬을 마치게 됩니다.
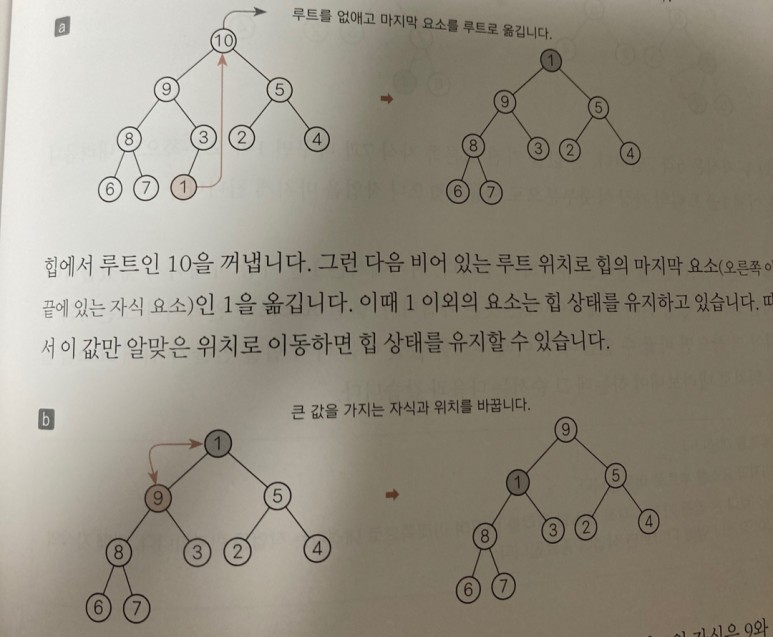
1) 루트를 꺼냅니다.
2) 마지막 요소를 루트로 이동합니다.
3) 자기보다 큰 값을 가지는 자식 요소와 자리를 바꾸며 아래쪽으로 내려가는 작업을 반복합니다. 이 때 자식의 값이
작거나 잎에 다다르면 작업이 종료됩니다.

[힙 정렬 알고리즘 살펴보기]
1. 변수 i의 값을 n-1로 초기화합니다.
2. a[0]과 a[i]를 바꿉니다.
3. a[0], a[1], ... , a[i-1]을 힙으로 만듭니다.
4. i의 값을 1씩 줄여 0이 되면 끝이 납니다. 그렇지 않으면 '2'로 돌아갑니다.

[힙 정렬의 시간 복잡도]
1. 힙 정렬에서는 첫 요소를 꺼내는 것만으로 가장 큰 값이 구해지므로 첫 요소를 꺼낸 다음 나머지 요소를 다시 힙으로 만들어야 그 다음에 꺼낼 첫 요소도 가장 큰 값을 유지합니다. 따라서 단순 선택 정렬에서 가장 큰 요소를 선택할 때의 시간 복잡도 O(n)의 값을 한번에 선택할 수 있어 O(1)로 줄일 수 있습니다. 그 대신 힙 정렬에서 다 시 힙으로 만드는 작업의 시간 복잡도는 O(log n)입니다.


downHeap 메서드
배열 a 가운데 a[left] ~ a[right]의 요소를 힙으로 만드는 메서드 입니다. a[left] 이외에는 모두 힙 상태라고 가정하고 a[left]를 아랫부분의 알맞은 위치로 옮겨 힙 상태를 만듭니다.
heapSort 메서드
요소의 개수가 n개인 배열 a를 힙 정렬하는 메서드입니다. 아래의 2단계로 구성됩니다.
1. downHeap 메서드를 사용하여 배열 a를 힙으로 만듭니다.
2. 루트(a[0])에 있는 가장 큰 값을 빼내어 배열 마지막 요소와 바꾸고 배열의 나머지 부분을 다시 힙으로 만드는 과정을 반복하여 정렬을 수행합니다.
'자바 Do,It 알고리즘(끝)' 카테고리의 다른 글
| [자바 Do It! 알고리즘]Chapter07 문자열 검색 (브루트-포스법) (0) | 2021.05.22 |
|---|---|
| [자바 Do It! 알고리즘]Chapter07 집합 (1)(배열로 집합 만들기) (0) | 2021.05.20 |
| [자바 Do It! 알고리즘]Chapter06 정렬 (병합 정렬-Arrays.sort로 퀵 정렬과 병합정렬하기) (0) | 2021.05.17 |
| [자바 Do It! 알고리즘]Chapter06 정렬 (병합 정렬) (0) | 2021.05.16 |
| [자바 Do It! 알고리즘]Chapter06 정렬 (비재귀적인 퀵 정렬) (0) | 2021.05.15 |



